滤波器嫁接技术：

Code： https://github.com/fxmeng/filter-grafting
Paper：https://arxiv.org/pdf/2001.05868.pdf

本文贡献：
提出了一种新的学习范式，称为滤波器嫁接。嫁接可以在不改变网络结构的情况下，重新激活无效的过滤器，提高神经网络的潜力。
提出了一种基于熵的准则和自适应加权策略，进一步提高了滤波器嫁接方法的性能。

1.滤波器嫁接动机

构建滤波器嫁接技术的动机是通常在训练完的网络中存在一些无效的滤波器，很多网络模型剪枝的文献中就会把这些无效的滤波器剪切掉。但是，这些看似无效的滤波器不一定是真的无效的，比如在集成学习中，当单个弱分类器效果差时，它们的组合反而会得到更强的性能。这说明无效的滤波器是可以被激活的，而本文考虑重新激活这些无效滤波器，在不增加模型推理时间的前提下，有效提升网络性能。

2.嫁接与裁剪，蒸馏的区别：

在这里插入图片描述

所谓的激活就是通过将外部信息移植到到这些无效滤波器中，该过程被定义为滤波器嫁接。滤波器嫁接的关键是选择合适的信息源

嫁接可能涉及并行地训练多个网络。因此，这个过程类似于蒸馏学习。嫁接和蒸馏的区别在于，蒸馏是一个两阶段的过程。首先，我们需要训练一个大模型(老师)，然后使用训练好的大模型来教一个小模型(学生)。而嫁接是一个单阶段的过程，在训练过程中进行滤波器嫁接。（优于传统蒸馏学习等方法）

if __name__ == '__main__':
    for epoch in range(start_epoch, args.epochs):
        train(epoch)
        test(epoch)
        state = {
            'net': net.state_dict(),
        }
        torch.save(state, '%s/ckpt%d_%d.t7' % (args.s, args.i % args.num, epoch))
        grafting(net, epoch)

3.如何计算滤波器的重要性

通常情况下多数裁剪文献中都利用L1范数来评价滤波器的重要性

L1范数（L1 norm）：

如下公式所示，以一层滤波器为单位，L1范数的计算就是将当前层滤波器中所有的卷积层参数进行逐点求绝对值并求和。现有的文献中普遍认为L1范数越接近零，当前滤波器越不重要。但最近的研究表明，更小更不重要的标准并不总是正确的。一个特殊的情况是，一个权重分布在 0–1之间的滤波器肯定比所有权重都为1的滤波器更好。很显然，L1范数准则只关注滤波器权值的绝对值，并没有关注权值的变化。因此利用L1范数评价滤波器的好坏是不全面的。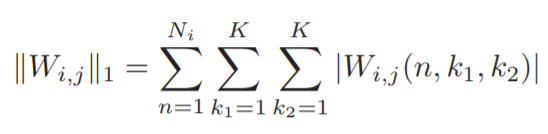

熵：

先概述一下计算过程。
分析了L1范数的利弊，我们发现用L1范数，滤波器不能区分输入的哪一部分更重要。所以我们选择测量权重的变化。本文提出了熵的形式来衡量滤波器权重的变化程度，以此为依据来判别滤波器的好坏。具体来说，计算熵的方法为将滤波器权重按照大小等分为离散的几个区间，并计算区间对应的概率，最后利用熵的公式计算整个滤波器的熵。如公式4，5结合起来，首先计算一层滤波器中一个卷积层的熵，并求和。公式6表示直接将当前层的滤波器进行权重划分后计算熵。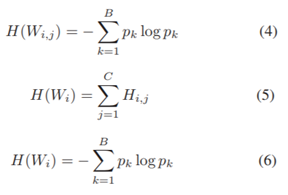

def entropy(x, n=10):
    x = x.reshape(-1)
    scale = (x.max() - x.min()) / n
    entropy = 0
    for i in range(n):
        p = torch.sum((x >= x.min() + i * scale) * (x < x.min() + (i + 1) * scale), dtype=torch.float) / len(x)
        if p != 0:
            entropy -= p * torch.log(p)
    return float(entropy.cpu())

下面我们依次对三个公式进行讲解：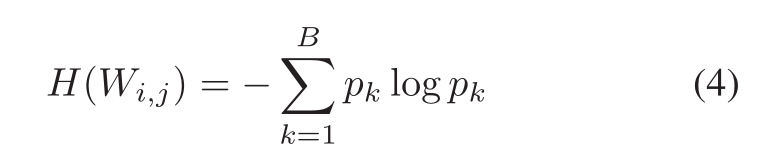

把滤波器的权重分为m个等大小的范围如：
0~~0.1 的大小是一个范围， 0.8~~0.9的大小是另一个范围。

计算每个范围中所含权重的个数占所有权重的比例如：
设一共有B个权重数据，有3个权重的大小刚好在0~0.1这个范围，那么这个时候Pk=3/B(这里的B与Pk与公式中的字母相对应）

如果滤波器的权重变化越小，Pk越小，则结果越小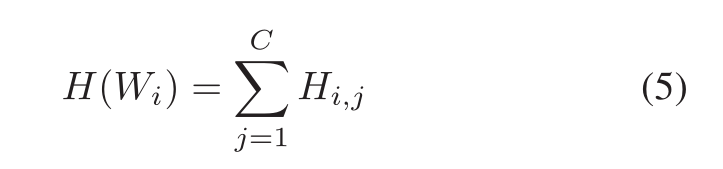

假设第i层有C个滤波器，那么第i层的总信息为（5）的计算结果（换个表达，把第i层中的C个滤波器的的信息加起来就可以得到该层的全部信息）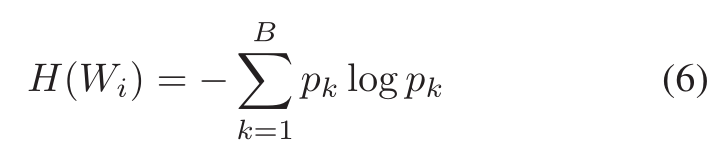

接下来就是要把每个层的信息进行关联，
我们采用与（4）相同的函数进行计算，与(4)不同的是，(6)中的值来自于整个层的权值，而不是单个过滤器。

4.滤波器嫁接详解

（1）噪声作为接穗

文章中作者将原始网络中无效的滤波器称为砧木，将有意义的滤波器称为接穗，这与嫁接的植物学解释是一致的。滤波器嫁接的目的是将信息(权重)从接穗转移到砧木，因此选择有用的信息是嫁接的关键。在本文中，作者提出了三种获取接穗的方法。

噪声作为接穗：利用均值为0，方差为delta的高斯噪声作为接穗，使得L1范数很小的无效滤波器变得更有效。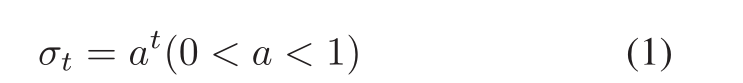

当然随着迭代次数的增加，需要适当降低高斯噪声方差的值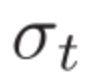，因为过大的方差会导致网络难以收敛。

2）内部滤波器作为接穗

我觉的可以直接从图中看出一个大概：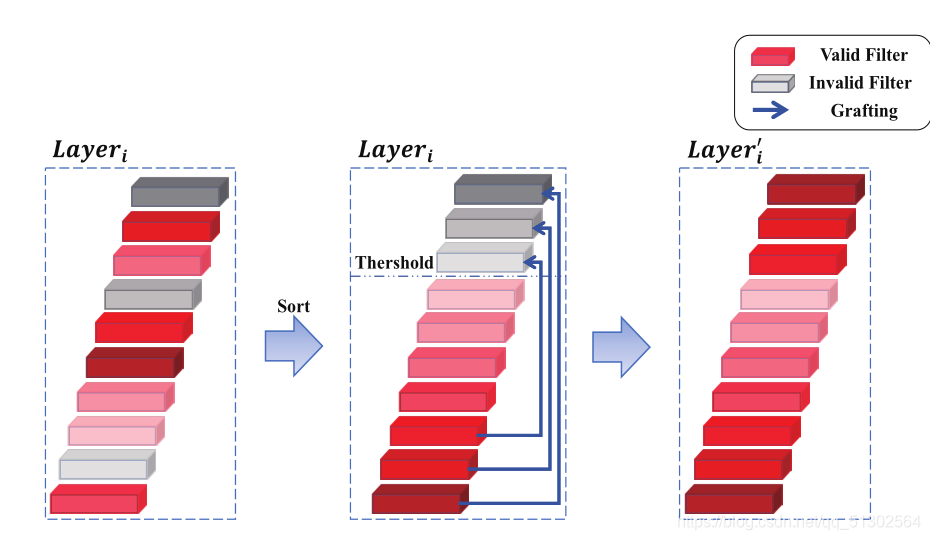

先计算熵值，然后按大小进行排序，接着对熵低于自己设定的阈值的通道i 将第i个熵值最大滤波器的权值移入第i个熵值最小滤波器( 滤波器的熵值小于γ，则认为这些滤波器是无效的)。由于这种嫁接技术发生在网络内部，因此无法增加额外的信息。

3）外部滤波器作为接穗

外部滤波器作为接穗：针对在单一网络中加入随机噪声和权值的缺点，可以从其他网络中选择外部滤波器作为接穗。具体来说，可以并行地训练两个网络(也可训练多个，这里先将两个的网络），分别记作M1和M2。在每个epoch的训练中，我们将M1的有效滤波器权值嫁接到M2的无效滤波器中。该过程中的嫁接发生在层级，而不是滤波器级，这意味着我们将M1中某一层中所有滤波器权重嫁接到同一层的M2中。（按我个人的理解，这两个网络应该是同一个网络，只是超参数的设置不同。欢迎有其他见解的人指出！）

在进行嫁接时，具体的操作如下公式所示，通过对接穗和砧木的权重进行加权后，得到最终的嫁接参数。其中阿尔法值要大于0.5，因为接穗的权重更有效。
（函数解析在图片后面哦）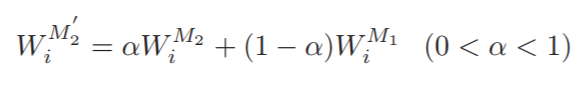

这里的权重系数阿拉法：
第一：当M2的熵值和M1的熵值相同时，阿尔法的值为0.5；当M2的熵值大于M1的熵值时，阿尔法的值大于0.5。
第二：即使M2的熵值和M1的熵值相差非常大的情况下，阿尔法的值也不能是0或无穷。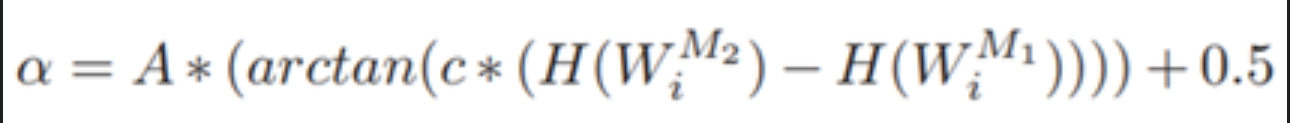

arctan函数（‘s形’，感觉可以理解为sigmoid函数的用法）把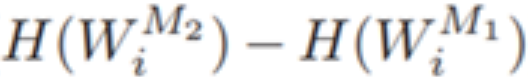
进行压缩，然后乘一个比例系数再加上0.5

def grafting(net, epoch):
    while True:
        try:
            checkpoint = torch.load('%s/ckpt%d_%d.t7' % (args.s, args.i - 1, epoch))['net']
            break
        except:
            time.sleep(10)
    model = collections.OrderedDict()
    for i, (key, u) in enumerate(net.state_dict().items()):
        if 'conv' in key:
            w = round(args.a / np.pi * np.arctan(args.c * (entropy(u) - entropy(checkpoint[key]))) + 0.5, 2)
        model[key] = u * w + checkpoint[key] * (1 - w)
    net.load_state_dict(model)